বিভিন্ন চাকুরির পরীক্ষায় বিশেষ করে PSC, SSC, Group-D, Clerkship প্রভৃতি পরীক্ষায় জ্যামিতি ও পরিমিতি থেকে যে সকল সমস্যা গুলি দেওয়া হয় সেগুলি সমাধানের জন্য কিছু প্রাথমিক জ্যামিতির ধারণা প্রয়োজন হয়। এই সহজ কিছু বিষয় না জানার ফলে অনেকেই জ্যামিতি ও পরিমিতির সমস্যাকে ভয় পায়। বিষয় গুলিকে সহজ করার জন্য আজকের এই আলোচনা।
জ্যামিতির প্রাথমিক বিষয় সমূহ
বিন্দু :
যে জ্যামিতিক চিত্রের দৈর্ঘ্য, প্রস্থ ও উচ্চতা কিছুই নেই, শুধুমাত্র অবস্থান আছে, তাকে বিন্দু বলে।
রেখা
কতকগুলি বিন্দু পাশাপাশি বসে যে চিত্র তৈরি হয় তাকে রেখা বলে। অন্য ভাবে বললে বলা যায় একটি বিন্দুর চলার পথ কে রেখা বলে।
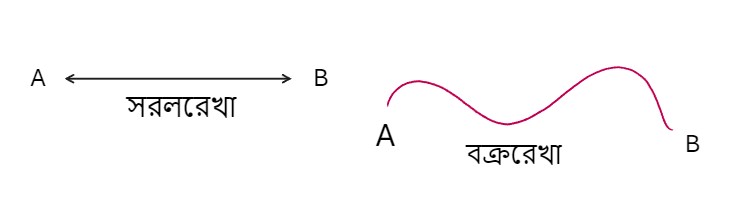
রেখা দুই প্রকার যথাঃ
- সরলরেখা
- বক্ররেখা
সরলরেখা কাকে বলে? যে রেখা তার চলার পথে কখনও দিক পরিবর্তন করে না, সর্বদা একই দিকে চলে তাকে সরল রেখা বলে।
বক্ররেখাঃ যে রেখা তার চলার পথে সর্বদা দিক পরিবর্তন করে তাকে বক্ররেখা বলে।
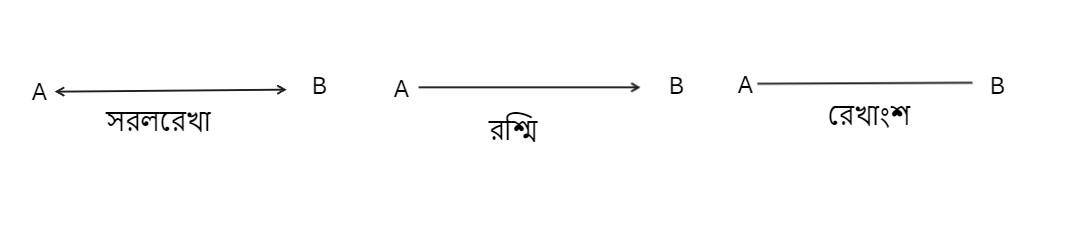
রশ্মি– সরলরেখার একপ্রান্ত স্থির এবং ওপর প্রান্ত যদি অসীম পর্যন্ত বিস্তৃত হয়, তবে তাকে রশ্মি বলে।
রেখাংশ- সরলরেখার যে অংশ উভয়দিকে প্রান্তবিন্দু দ্বারা সীমাবদ্ধ তাকে রেখাংশ বলে।
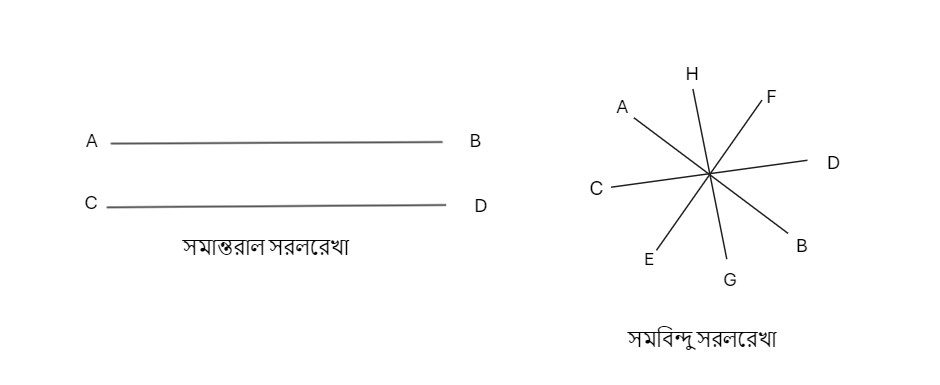
সমান্তরাল সরলরেখাঃ একই সমতলে দুই বা তার বেশি সরলরেখার মধ্যবর্তী দূরত্ব যদি সর্বদা সমান থাকে এবং এদের উভয় দিকে যত খুসি বর্ধিত করলেও এরা কখনো পরস্পরকে ছেদ না করে তবে তাদের সমান্তরাল সরলরেখা বলে।
সমবিন্দু সরলরেখাঃ একই সমতলে যদি একাধিক সরলরেখা একটি বিন্দুতে মিলিত হয় তবে তাদের সমবিন্দু সরলরেখা বলে।
সমরেখ বিন্দুঃ যদি তিন বা তার বেশি বিন্দু একই সরলরেখায় থাকে তবে তাদের সমরেখ বিন্দু বলে। অন্যথায় তাদের অসমরেখ বিন্দু বলে।
সামতলিক ক্ষেত্রঃ এক বা একাধিক রেখা দ্বারা আবদ্ধ ক্ষেত্রকে বা চিত্রকে সামতলিক ক্ষেত্র বলে। সামতিক ক্ষেত্রের পরিসীমা ও ক্ষেত্রফল পরিমাপ যোগ্য। এদের কোন আয়তন হয়না। কারন সামতলিক ক্ষেত্রের সমতলের বাইরে কোন অস্তিত্ব নেই। অর্থাৎ এদের কোন উচ্চতা নেই। উদাহরণ স্বরূপ ত্রিভুজ, আয়তক্ষেত্র, বর্গক্ষেত্র, বৃত্ত এগুলি হল সামতলিক ক্ষেত্র।
ত্রিভুজঃ তিনটি বাহু দ্বারা সীমাবদ্ধ ক্ষেত্রকে ত্রিভুজ বলে। 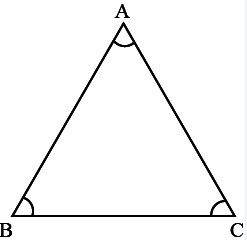
বাহু ভেদে ত্রিভুজ তিন প্রকার। যথাঃ-
- 1. সমবাহু ত্রিভুজ,
- 2. সমদ্বিবাহু ত্রিভুজ,
- 3. বিষমবাহু ত্রিভুজ

সমবাহু ত্রিভুজ– যে ত্রিভুজের তিনটি বাহুর দৈর্ঘাই সমান তাকে সমবাহু ত্রিভুজ বলে।
সমদ্বিবাহু ত্রিভুজ- যে ত্রিভুজের যে-কোনো দুটি বাহুর দৈর্ঘ্য সমান তাকে সমদ্বিবাহ্ ত্রিভুজ বলে।
বিষমবাহু ত্রিভুজ– যে ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যই অসমান তাকে বিষমবাহু ত্রিভুজ বলে।
কোণ ভেদে ত্রিভুজ তিন প্রকার। যথা-
- 1. সূক্ষ্মকোণী ত্রিভুজ,
- 2. সমকোণী ত্রিভুজ,
- 3. স্থুলকোণী ত্রিভুজ।
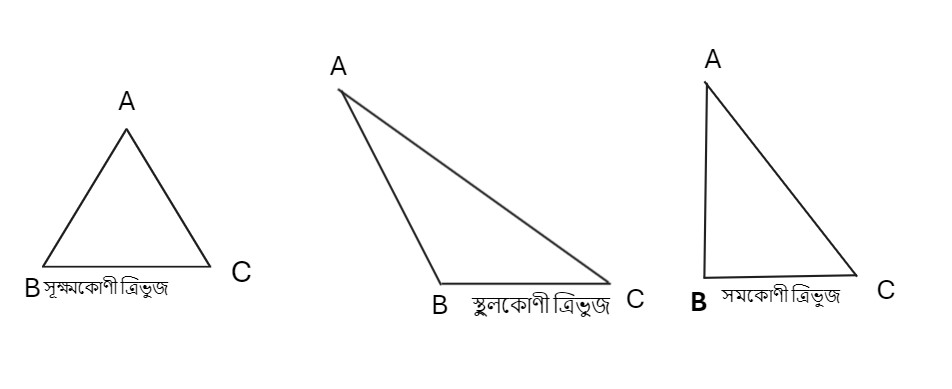
সূক্ষ্মকোণী ত্রিভুজ– যে ত্রিভুজের তিনটি কোণই সূক্ষ্মকোণ হয় তবে তাকে সূক্ষ্মকোণী ত্রিভুজ বলে।
সমকোণী ত্রিভুজ– যে ত্রিভুজের একটি কোণ সমকোণ তাকে সমকোণী ত্রিভুজ বলে।
স্থুলকোণী ত্রিভুজ– যে ত্রিভুজের একটি কোণ স্থুলকোণ তাকে স্থুলকোণী ত্রিভুজ বলে।
চতুর্ভুজঃ চারটি বাহু দ্বারা সীমাবদ্ধ ক্ষেত্রকে চতুর্ভুজ বলে। 
বৃত্তঃ যদি কোন সামতলিক ক্ষেত্র একটিমাত্র বক্র রেখা দ্বারা এমন ভাবে বেষ্টিত হয় যে, তার মধ্যে অবস্থিত কোন নির্দিষ্ট বিন্দু থেকে ঐ বক্ররেখার উপর অবস্থিত যে কোন বিন্দুর দূরত্ব সর্বদা সমান তবে ঐ সামতিক ক্ষেত্রকে বৃত্ত বলে। বৃত্ত মধ্যস্থিত ঐ নির্দিষ্ট বিন্দুকে ঐ বৃত্তের কেন্দ্র বলা হয়। এবং কেন্দ্র থেকে বক্ররেখা পর্যন্ত দূরত্বকে ঐ বৃত্তের ব্যাসার্ধ বলা হয়।
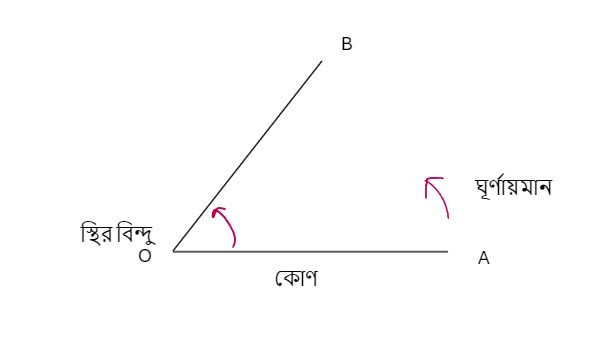
কোণ Angle:
যদি একটি সরলরেখার একটি প্রান্ত স্থির এবং ওপর প্রান্ত ওই স্থির বিন্দু সাপেক্ষে ঘূর্ণায়মান হয়, তবে ওই স্থির বিন্দু সাপেক্ষে সরলরেখাটির প্রাথমিক ও অন্তিম অবস্থানের মধ্যবর্তী দূরত্বকে কোণ বলে।
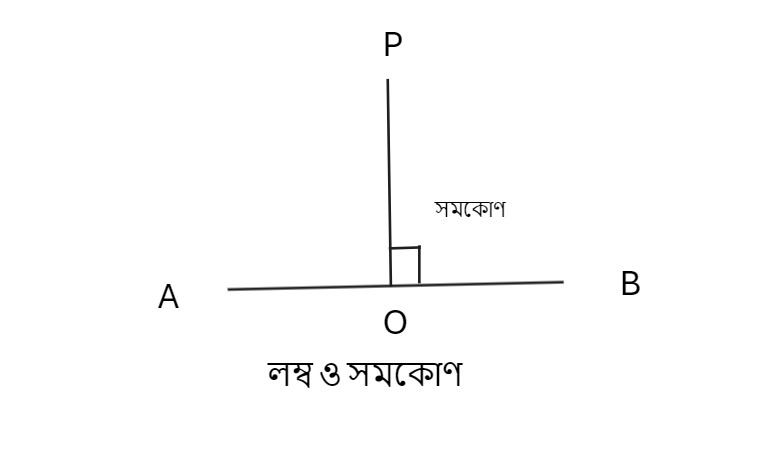
সমকোণ ও লম্ব –
যদি একটি সরলরেখার উপর ওপর একটি সরলরেখা দণ্ডায়মান হয় (দাড়ায়), এবং এর ফলে উৎপন্ন সন্নিহিত কোণ দুটি সমান হয় তবে ওই কোণ দুটির প্রত্যেককে সমকোণ বলা হবে এবং সরলরেখা দুটির একটিকে অপরটির লম্ব বলা হবে।
একটি ঘূর্ণায়মান সরলরেখা একটি বিন্দুর চারপাশে মোট চার সমকোণ কোণ উৎপন্ন করে যা 360° এর সমান। তাই এক সমকোণ = 90°.
বিভিন্ন প্রকার কোণ
সূক্ষ্মকোণ– যে কোণের মান এক সমকোণ অপেক্ষা কম অর্থাৎ 90° এর কম তাকে সূক্ষ্মকোণ বলে।
স্থুলকোণ– যে কোণের মান এক সমকোণ অপেক্ষা বেশি কিন্তু দুই সমকোণ অপেক্ষা কম (অর্থাৎ 90° থেকে 180° এর মধ্যে) তাকে স্থুলকোণ বলে।
সরলকোণ– দুই সমকোণকে এক সরল কোণ বলে অর্থাৎ 180° কোণকে সরলকোণ বলে।
প্রবৃদ্ধ কোণ – যে কোণের মান 180° এর বেশি তাকে প্রবৃদ্ধ কোণ বলে।
